Límite inferior del intervalo clase modal : Cómo calcular la moda o el valor modal.

Calcular Cualquier: Promedio, Media Y Moda, De Una Lista De Datos

= límite inferior de la clase modal.

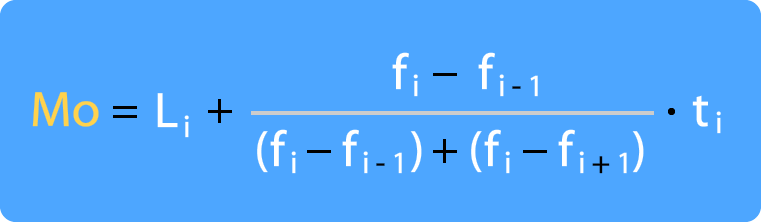
Formula de la moda estadistica. La moda \(m_o\) es el valor más probable o frecuente, es decir, el valor con mayor probabilidad, si la variable es discreta, o el valor que maximiza la función de densidad si es continua. Cuando los intervalos tienen amplitudes distintas. La media aritmética es el promedio de un conjunto de números, a 1, a 2, a 3,.

Li es el limite inferior del intervalo con mayor frecuencia absoluta. Contabiliza cuantas veces se repite cada valor. En estadística, la moda es el valor con mayor frecuencia en una distribución de datos.

Cálculo de la moda para valores agrupados en intervalos. Veamos algún ejemplo del cálculo de la moda: 3° calculemos la moda m o :

Mide la distancia entre los valores de la serie y la media, se calcula a través de la sumatoria de las diferencias al cuadrado entre los valores y la media, multiplicándose por el número de veces que se ha repetido, ese sumatorio final que obtienes lo divides con el tamaño de la muestra. 9, 11, 9, 9, 13, 11, 12. En el caso de una única moda se dice que la distribución es unimodal, y con más modas multimodal.

Por lo tanto, para calcular la moda de un conjunto de datos estadísticos basta con contar el número de veces que aparece cada dato en la muestra, y el dato más repetido será la moda. Aplicaremos la fórmula para el cálculo de la moda para datos agrupados, extrayendo los siguientes datos: Cálculo de la moda para datos agrupados.

¿cómo calcular la moda en datos no agrupados? F i es la frecuencia absoluta de la clase modal. Ordena tus datos de forma ascendente o descendente.

Antes de calcularla, definimos la moda como el valor que más se repite dentro de una distribución de datos. 1) buscamos la clase modal (intervalo con mayor frecuencia) 2) aplicamos la siguiente fórmula:: La formula que usaremos para el cálculo de la moda, en el caso de que tengamos datos agrupados será:

¿cómo se calcula la moda? Ahora podemos reemplazar los datos en la fórmula: Se hablará de una distribución bimodal de los datos adquiridos en una columna cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima.

Frecuencia absoluta del intervalo modal : Para calcular el valor modal de una serie de números sólo tienes que ordenar los valores y reconocer cuál es que el aparece con más frecuencia. Vemos que el valor 9 se repite 3 veces, más que cualquier otro, por lo tanto:

También puede darse el caso a la inversa y. Aplicaremos la fórmula para el cálculo de la moda para datos agrupados, extrayendo los siguientes datos: La moda estadística de un conjunto de datos, se define como el número que está representado más veces dentro de esos datos, es decir, aquel número que presenta una mayor frecuencia absoluta dentro de la muestra.

Para encontrar el modo aplicaremos la siguiente formula: ., a n, obtenida sumando todos los números y dividiéndola entre n. En estadística, la moda es el valor del conjunto de datos que tiene una mayor frecuencia absoluta, es decir, la moda es el valor que más se repite de un conjunto de datos.

Frecuencia absoluta del intervalo siguiente al modal Frecuencia absoluta del intervalo anterior al modal : = es el delta de frecuencia absoluta modal y la frecuencia absoluta postmodal.

Para obtener la moda en datos agrupados se usa la siguiente fórmula: Veamos un ejemplo de valor modal para verlo más claro: 9, 9, 9, 11, 11, 12, 13.

La moda no tiene por qué ser única. La moda (mo) es el valor x i que tiene la mayor frecuencia absoluta. Una distribución trimodal de los datos es en la que encontramos tres modas.

La moda puede ser calculada tanto para variables cuantitativas como para variables cualitativas. Dichos datos pueden ser agrupados o no agrupados. Se aplica la fórmula para calcular la moda en datos agrupados:

A continuación, el procedimiento para ambos tipos de datos: 4 calcular la moda de una distribución estadística que viene dada por. Si la moda está en el último intervalo, entonces f i+1 = 0.

La moda es una medida de tendencia central que indica el valor que más se repite en un grupo de números. En caso de una variable continua será la clase modal o para hacerlo de una forma. M o = 30 + 3, 57.

Modo de una serie estadistica de intervalos. Mo = li + d1 * i. En un mismo estudio puede haber más de una moda, esto ocurre cuando dos (bimodal) o más números (multimodal) se repiten la misma cantidad de veces siendo este es el máximo número de veces del conjunto.

Lo primero que debemos hacer es identificar el intervalo modal: Por lo tanto, la moda es: 1º todos los intervalos tienen la misma amplitud.

= es el delta de frecuencia absoluta modal y la frecuencia absoluta premodal. Para este cálculo de la moda estadística aplicamos los siguientes pasos: Calcular la moda de los siguientes precios de un kilo de manzanas en diferentes supermercados:

Para obtener la moda estadística en datos agrupados haremos uso de la fórmula: L i {\displaystyle l_ {i}} = límite inferior de la clase modal. (media aritmética) = (a 1 +a 2 +a 3 +.

= amplitud del intervalo modal ejemplos para calcular la moda. Formula de la moda para datos agrupados. D 1 {\displaystyle d_ {1}}

M = l i + ( d 1 d 1 + d 2 ) a i {\displaystyle m=l_ {i}+\left ( {\frac {d_ {1}} {d_ {1}+d_ {2}}}\right)a_ {i}} donde: Ordenamos los valores de menor a mayor:

La estadística se divide en dos elementos: Estimadores que son medidas referentes a la muestra como la media ( x ) o la varianza s2 y parámetros que son los equivalentes poblacionales de los estimadores.

Protocolo 1

Su objetivo era facilitar la gestión de las labores tributarias, obtener datos sobre el número de personas que podrían servir en el ejército o establecer repartos de tierras o de otros bienes.

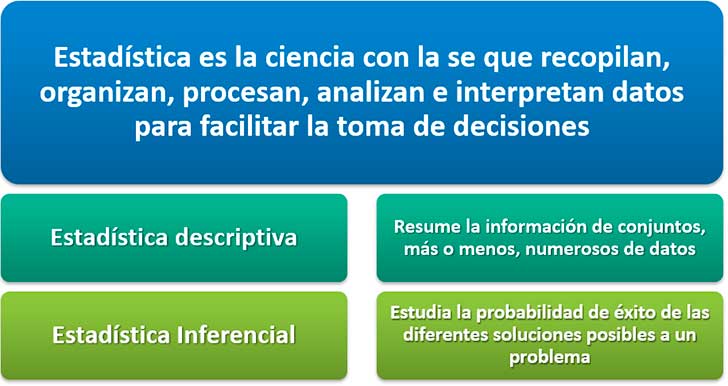
Como se divide la estadistica. La función descriptiva de la estadística se enfoca en la presentación y clasificación de los datos obtenidos de la población que se analiza. Rama de las matemáticas que se ocupa de reunir, organizar y analizar datos numéricos y que ayuda a resolver problemas como el diseño de experimentos y la toma de decisiones. Al estudio completo de la población.

La estadística es una de las ciencias que presenta gran dificultad en la posibilidad de definirla, ya que la misma, presenta un objeto de estudio bastante complejo, las cantidades que puedan mutar de la ocurrencia de un fenómeno. Los datos pueden ser resumidos numérica o gráficamente. Estadística inferencial se dedica a la generación de los modelos, inferencias y predicciones asociadas a los fenómenos en

¿como se divide la estadística ? La estadística descriptiva resume la información contenida en los datos recogidos y la estadística inferencial demuestra asociaciones y permite hacer comparaciones entre características observadas. Dicho en otras palabras, son los antecedentes (en cifras) necesarios para llegar al conocimiento de un hecho o para.

La estadística descriptiva, la cual se relaciona con la descripción de los datos recopilados en una muestra, y la estadística inferencial, que se relaciona con el proceso de utilizar los datos de una muestra para realizar inferencias y tomar decisiones respecto a la población de. La estadística descriptiva, la cual se relaciona con la descripción de los datos recopilados en una muestra, y la estadística inferencial, que se relaciona con el proceso de utilizar los datos de una muestra para realizar inferencias y tomar decisiones respecto a la población de. La inferencial y la descriptiva.

Se divide en dos grandes ramas, la bioestadística descriptiva y la bioestadística analítica o inferencial. La estadística se divide en dos ramas: Un subconjunto representativo seleccionado de una población de la cual se obtuvo.

Estadística descriptiva se dedica a los métodos de recolección, descripción, visualización y resumen de datos originados a partir de los fenómenos en estudio. Clasificación de la estadística inferencial. Ciencia que utiliza conjuntos de datos numéricos para obtener, a partir de ellos, inferencias basadas en el cálculo de probabilidades.

O deductiva se construye a partir de los datos y la inferencia sobre la población no se puede realizar, al menos con una confianza determinada, la representación de la información obtenida de los datos se representa mediante. La estadística, por su aplicación se divide en: Así por ejemplo, en un análisis paramétrico podemos trabajar bajo el supuesto de que la población se distribuye como una normal (hay que justificar nuestro supuesto) y luego sacar conclusiones bajo el.

Lo constituyen las características medibles en una población completa. Luego de investigar, estudiar y analizar con los métodos anteriores, se utiliza la estadística aplicada para proporcionar resultados específicos y generalizados sobre la investigación. Otros la definen como la.

La estadística se clasifica en 2 ramas : En el oriente medio, bajo el dominio sumerio, babilonia tenía casi 6000 habitantes. La estadística descriptiva, la cual se relaciona con la descripción de los datos recopilados en una muestra, y la estadística inferencial, que se relaciona con el proceso de utilizar los datos de una muestra para realizar inferencias y tomar decisiones respecto a la población de la cual se toma la muestra.

¿cómo se divide la estadística? La estadística descriptiva, que se dedica a los métodos de recolección, descripción, visualización y resumen de datos originados a partir de los fenómenos en estudio. La estadística se divide en dos ramas:

Para chacón esta se define como “la ciencia que tiene por objeto el estudio cuantitativo de los colectivos”; Además de estas dos áreas, existe la estadística matemática, la cual comprende las bases teóricas de la estadística. La estadística se divide en dos ramas:

El estudio de la estadística se divide Ejemplos básicos de descriptores numéricos son la media y la desviación. Se le asigna un símbolo representado por una letra griega.

La estadística se divide en dos grandes áreas: Nombre del patrocinante de la encuesta, (oficial o privada), nombre de la encuesta, número del cuestionario, nombre del encuestador, lugar y fecha de la entrevista. Es la medida de una.

Se caracteriza porque asume que los datos tienen una determinada distribución o se especifican determinados parámetros que deberían cumplirse. En la edad antigua, la estadística consistía en elaborar censos (de población y tierras.). Ingrid figueroa flores ruy uriel amaro goiz ¿que es la estadística?

Estadística descriptiva y estadística inferencial, las cuales comprenden la estadística aplicada. La estadística se divide en dos ramas :la estadística descriptiva , la cual se relaciona con la descripción de los datos recopilados en una muestra ,y la estadística inferencial,que se relaciona con el proceso de utilizar los datos de una muestra para realizar inferencias y tomar decisiones respecto a la población. Al estudio de la muestra representativa.

La estadística inferencial se divide según el tipo de variables que tenemos: La estadística se clasifica en dos grandes ramas conocidas como esta dística descriptiva y estadística inferencial. La estadística se divide en dos ramas:

Como se divide la estadística. Se representan los valores de la frecuencia: Además de realizar los procesos de estadística deductiva o inferencial, la estadística matemática utilizará el álgebra y ciertos análisis más profundos para.

Scribd es red social de lectura y publicación más importante del mundo. Estadística paramétrica, está basada en dos supuestos:

Y = a + bx + u. La observación de la nube de puntos nos da una idea de cuál puede ser el modelo funcional más apropiado para describir la relación entre las variables y también nos permite.

Coeficiente De Correlación De Pearson - Wikipedia, La Enciclopedia Libre

Suponga que cada observación es y xi donde 'x' indica la categoría a la que pertenece la observación, 'i' es la etiqueta de la observación en particular.

Medidas de correlacion en estadistica. El coeficiente de correlación de pearson es adecuado para datos cuantitativos de intervalo o razón. En caso de que suceda, diremos que las variables están correlacionadas o que hay correlación entre ellas. Es decir, determinar si los cambios en una de las variables influyen en los cambios de la otra.

Por tanto, usualmente las correlaciones se escriben con dos números clave: Es un dataframe con al menos 2 variables (2 columnas). Existen varios tipos de correlacin que pueden calcularse y dependen de la escala de medicin en que se hallan medido cada una de las variables, enfatizando que la escala ms fuerte es la de razn por lo que la estructura general se obtiene bajo este.

Las medidas de correlación se aplican a los valores que toman dos variables distintas en cada uno de los elementos de una muestra, y expresan si ambas variables varían a la vez, es decir, si los valores de una son más altos o bajos cuanto más altos o bajos son los de la otra. El valor p es una medida de probabilidad empleada para hacer pruebas de hipótesis. Es decir, determinar si los cambios en una de las variables influyen en los cambios de la otra.

Es un vector (numérico o carácter) que indica las variables a seleccionar de x.si x solo tiene 2 variables (columnas), variable = null.en caso contrario, es necesario indicar el nombre o posición (número de columna) de las variables a seleccionar. 1 medidas de correlacion para medir el grado de asociacin entre dos o ms variables se utilizan los coeficientes de correlacin. Dos variables están relacionadas cuando al variar los valores de una variable también cambian los valores de la otra variable.

En caso de que suceda, diremos que las variables están correlacionadas o que hay correlación entre ellas. La significancia estadística se indica mediante un valor p. Digamos que n x es el número de.

La correlación indica el grado de relación lineal entre 2 variables numéricas. Se trata de un dato esencial para interpretar los resultados de nuestro estudio y su ausencia en los artículos científicos se ha identificado como uno de los 7 fallos más comunes en investigación (según la apa 19961 , 20012 ). La correlación es una medida estadística que indica el grado de relación entre dos variables.

Si tenemos dos variables existe correlación entre ellas si al. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores homónimos de la otra: El coeficiente de correlación es una medida del tamaño del efecto para la relación (lineal) entre dos variables numéricas.

Es decir, determinar si los cambios en una de las variables influyen en los cambios de la otra. El punto de partida de un estudio de correlación es la representación gráfica de los pares de valores relacionados en un sistema cartesiano: Si los valores de ambas variables aumentan o disminuyen a la vez, su correlación es positiva;

Se obtiene así el diagrama de dispersión o nube de puntos. El signo negativo indica relación lineal decreciente. En tanto, en probabilidad y estadística, la correlación es aquello que indicará la fuerza y la dirección lineal que se establece entre dos variables aleatorias.

El signo positivo indica relación lineal creciente. De hecho, formulamos dos hipótesis: En el caso de variables nominales, ordinales o dicotómicas se usan otros coeficientes, aunque algunos de ello se reducen en sus cálculos al coeficiente de pearson.

La correlación es en esencia una medida normalizada de asociación o covariación lineal entre dos variables. En estadística, la razón de correlación es una medida de la relación entre la dispersión estadística entre categorías individuales y la dispersión entre la muestra o la población completa. La correlación determina la relación o dependencia que existe entre las dos variables que intervienen en una distribución bidimensional.

La correlación trata de establecer la relación o dependencia que existe entre las dos variables que intervienen en una distribución bidimensional. Si la correlación es igual a. Observamos varias veces el tiempo que tarda un móvil en recorrer una distancia y su velocidad (supuesto que se desplaza con velocidad uniforme), los valores observados están claramente relacionados y esa relación puede expresarse matemáticamente como v = s / t (v t = s).

En probabilidad y estadística, la correlación indica la fuerza y la dirección de una relación lineal y proporcionalidad entre dos variables estadísticas. En el análisis de correlación, usualmente, la hipótesis nula expresa que la. El objetivo de una prueba de hipótesis es determinar si hay evidencia suficiente para apoyar una determinada hipótesis sobre los datos.

El coeficiente de correlación es una medida estadística que calcula la fuerza de la relación entre los movimientos relativos de dos variables. La hipótesis nula y la hipótesis alternativa. Uso cuando dos variables de tipo cuantitativo presentan correlación la una respecto de la otra cuando los valores de una ellas varíen sistemáticamente con respecto a los valores homónimos de la otra.

En concreto, la correlación lineal sirve para determinar cuánto de correlacionadas linealmente están dos variables distintas. La correlación estadística determina la relación o dependencia que existe entre las dos variables que intervienen en una distribución bidimensional.